Ce billet est un avis de recherche de documents, livres en particulier, donnant des éléments de réponses à des questions qui me hantent depuis que j’exerce le métier d’enseignant. Si vous avez des lectures émanant de spécialistes en sciences de l’éducation, neurosciences, sciences cognitives à me recommander, merci de me contacter via twitter @OlivierBailleux, où à mon adresse email olivier [point] bailleux [at] u-bourgogne [point] fr.

Une question centrale

J’aimerais savoir ce que nous disent les connaissances scientifiques actuelles sur l’art et la manière d’apprendre à réfléchir, à comprendre, à raisonner, à décortiquer un problème, à déduire, à généraliser, à s’approprier intellectuellement un paradigme ou une théorie, à poser les questions dont les réponses permettront d’optimiser la quantité de connaissance récupérée, à exploiter les réponses pour optimiser notre apprentissage.

Comment peut-on aider des gens à développer ces compétences afin de leur permettre de gagner en autonomie, vitesse, efficacité et qualité d’apprentissage ?

Je prends un exemple concret. Voici une règle connue par beaucoup de gens, qu’on pourrait appeler la règle de la multiplication par 10 :

Pour multiplier un nombre entier par 10, on ajoute 0 à la fin.

Il s’agit d’une connaissance superficielle. Un principe qui permet, de manière mécanique, de réaliser une multiplication par 10. Je voudrais que mes élèves soient capables de cerner, d’approfondir, de comprendre, d’analyser, de généraliser les connaissances sous-jacentes.

Cerner

La règle présentée ci dessus est rédigée de manière imprécise. Une personne cernant exactement ce que dit cette règle devrait être capable de la reformuler de manière plus précise, par exemple de la manière suivante :

En ajoutant le chiffre 0 à la fin de la représentation décimale d’un entier x, on obtient la représentation décimale de dix fois x.

Cerner le sens profond de cette phrase suppose de comprendre différentes notions sous-jacentes :

• Comprendre ce que sont les objets mathématiques appelés entiers naturels.
• Comprendre ce qu’est la fonction qui à tout couple (x,y) d’entiers naturels associe un entier naturel appelé produit de x par y.
• Comprendre qu’il existe différentes manières de représenter les entiers naturels.
• Comprendre le principe d’une de ces représentations, appelée représentation décimale.
• Comprendre que le calcul du produit de deux entiers quelconques, appelé multiplication, suppose un algorithme (une méthode de calcul) qui s’applique à des représentations de ces entiers et retourne une représentation du résultat.
• Comprendre qu’en représentation décimale, ajouter le caractère 0 à la fin de la représentation d’un entier naturel x permet de réaliser une multiplication de x par l’entier naturel dont la représentation 10.

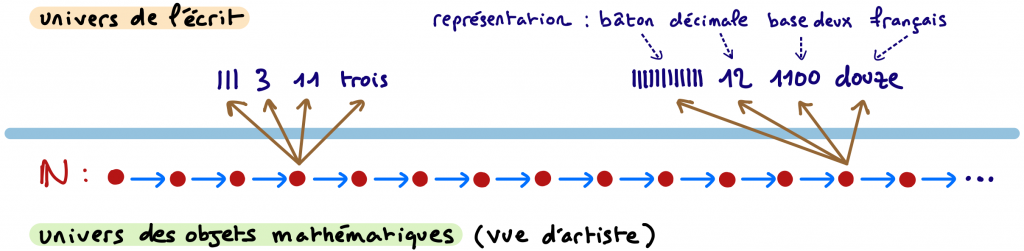
Sans une compréhension limpide de ces notions et de leurs prérequis, on ne peut appréhender que de manière partielle, incomplète, le sens de la règle de multiplication par 10, même si on est parfaitement capable de l’appliquer. En particulier, beaucoup de gens ne distinguent pas un nombre de sa représentation décimale. Ces personnes considèrent un nombre et sa représentation écrite en base 10 comme étant un même objet, ce qui n’est pas gênant dans la vie courante, mais peut être source d’erreurs lors de la conception de certains programmes informatiques, par exemple.

Mes attendus de la part des élèves :

Qu’iels soient capables de discerner différents niveaux d’abstraction, de faire correspondre les termes utilisés avec ces niveaux d’abstraction. Par exemple un entier naturel et sa représentation décimale ne sont pas au même niveau d’abstraction. Qu’iels aient une démarche exploratoire, se posent des questions, établissent des connexions entre les concepts nouveaux et les concepts déjà connus, raffinent en permanence leur vision d’un domaine ou d’un sujet en le revisitant avec un regard nouveau, expriment leurs connaissances de manière aussi limpide que possible en utilisant des écrits et des schémas.

Comprendre en profondeur

Pourquoi la règle de la multiplication par 10 fonctionne ? Pourquoi l’ajout d’un 0 à la fin de la représentation décimale d’un nombre entier réalise une multiplication par 10 ? Comment peut-on être sûr qu’il n’y a pas quelques exceptions ?

Dans la représentation décimale d’un entier, chaque chiffre a un poids, qui est une puissance de 10. En allant de droite à gauche, les poids successifs sont 1, 10, 100, etc.

L’insertion du chiffre 0 à droite a pour effet de décaler tous les autres chiffres d’une position vers la gauche, donc de multiplier leurs poids par 10.

Un entier a pour valeur la somme des produits des valeurs des chiffres de sa représentation décimale par leurs poids respectifs. Le décalage à gauche de tous les chiffres avec insertion du chiffre 0 à droite a donc pour effet une multiplication par 10 de l’entier représenté.

Mes attendus de la part des élèves :

Qu’iels soient capables de construire et de comprendre une explication précise et rigoureuse de la raison pour laquelle la méthode proposée réalise l’opération indiquée.

Explorer et étendre le champ d’utilisation

La règle peut avoir des utilisations dérivées.

Que se passe-t-il si on ajoute un chiffre autre que 0, par exemple 5, à la fin de la représentation décimale d’un entier ?

Quel est l’effet de supprimer le dernier chiffre de la représentation décimal d’un entier ?

Comment peut-on rapidement obtenir le quotient et le reste de la division par 10 d’un entier ?

La méthode est-elle applicable pour multiplier ou diviser un entier avec d’autres valeurs que 10 ? Lesquelles ?

La règle de la multiplication par 10 fonctionne-t-elle avec les entiers relatifs (pouvant avoir des valeurs positives ou négatives) ? Pourquoi ?

Mes attendus de la part des élèves :

Qu’iels soient capables, en s’appuyant sur une compréhension en profondeur des principes sous-jacents à une méthode ou une propriété connue, d’en élargir l’utilisation ou de s’en inspirer pour trouver des moyens de résoudre des problèmes différents de celui initialement adressé.

Généraliser

Et si on change de base ? Si, par exemple, on travaille avec des représentations des entiers naturels en base 2, plutôt qu’en base 10, quel est l’effet d’ajouter le chiffre 0 à la fin de la représentation d’un nombre ?

Quelles sont les opérations arithmétiques réalisables par des décalages à droite où à gauche des chiffres de représentations d’entiers naturels dans une base b donnée ?

Comment adapter la méthode pour la rendre applicable à des nombres rationnels (pouvant s’écrire sous la forme d’une fraction a/b) ? À des nombres représentés par une partie entière et une partie fractionnaire située après une virgule ?

Mes attendus de la part des élèves :

Qu’iels soient capables de discerner un principe général et de l’instancier dans des situations nouvelles ou dans un contexte différent de ceux dans lesquels ce principe a été présenté, exemplifié et utilisé.

Créer

On dispose d’un langage de programmation permettant de réaliser des opérations arithmétiques sur des entiers. La représentation des entiers utilisée par ce langage n’a aucune importance.

On veut réaliser un programme qui accepte en entrée trois entiers nommés x, b et i et produit en sortie la valeur du chiffre situé en position i (en numérotant les positions à partir de 0, de gauche à droite) dans la représentation en base b de l’entier x.

Mes attendus de la part des élèves :

Qu’iels soient capables d’inventer, de concevoir une méthode, un algorithme, un programme permettant de résoudre un problème qu’iels n’ont encore jamais rencontré en utilisant des briques de construction dont les rôles et fonctionnements sont connus et maîtrisés.

Quelques questions dérivées

Le poème de Nicolas Boileau

Certains vers du chant 1 du célèbre méta-poème « L’art poétique » de Nicolas Boileau semblent très inspirants pour une personne enseignante, comme par exemple :

Avant donc que d’écrire apprenez à penser.

Selon que notre idée est plus ou moins obscure,

L’expression la suit, ou moins nette, ou plus pure.

Ce que l’on conçoit bien s’énonce clairement,

Et les mots pour le dire arrivent aisément.

Ou encore :

Travaillez à loisir, quelque ordre qui vous presse.

Et ne vous piquez point d’une folle vitesse

…

Hâtez-vous lentement ; et, sans perdre courage,

Vingt fois sur le métier remettez votre ouvrage :

Polissez-le sans cesse et le repolissez ;

Ajoutez quelquefois, et souvent effacez.

Ce poème a-t-il été étudié à l’aune des connaissances actuelles en sciences de l’éducation ? Est-ce une bonne idée d’y faire référence dans le cadre de la communication avec des personnes apprenantes ?

La puissance de l’écrit

La maîtrise du langage, et en particulier du langage écrit est-elle déterminante dans l’acquisition des compétences de haut niveau décrites précédemment ?

Si oui, faut-il développer l’enseignement du langage technique pour faciliter ensuite ces apprentissage ? À quelles étapes des parcours scolaires et universitaires ?

Y-a-t-il un bénéfice à demander aux élèves d’expliquer, de restituer, de résumer sous forme écrite les connaissances qu’iels ont acquises ou qui sont en cours d’acquisition ?

La puissance du dessin

Faut-il inciter les élèves à s’exprimer sous forme graphique, à réaliser des schémas et des dessins pour représenter les notions et concepts qu’iels doivent assimiler ? Le dessin peut-il faciliter la compréhension en profondeur d’un système complexe ou d’un objet abstrait ?

Le fait de réfléchir en s’appuyant sur des représentations graphiques est-il universellement bénéfique ou peut-il être contreproductif chez certaines personnes ?

La puissance du brouillon

Peut-on enseigner aux élèves comment utiliser un espace de brouillon (feuille, écran, tablette, tableau) pour étendre leur mémoire de travail et accélérer leur compréhension en profondeur, leurs apprentissages, leur capacité à résoudre des problèmes ?

Si c’est souhaitable, comment peut-on l’enseigner ? Comment peut-on amener les gens à utiliser un brouillon de la meilleure manière possible ?

L’ingénierie, une pensée à part ?

Y a-t-il des manières de penser spécifiques à certains domaines, tels que par exemple les mathématiques ou l’ingénierie (c’est à dire l’art de concevoir des système complexes à partir de briques de construction connues et maîtrisées, en décomposant ces systèmes en blocs ayant des rôles clairement définis et interagissant entre-eux pour produire l’effet recherché) ?

Comment amener les élèves à développer le mode de pensée adapté aux compétences qu’iels doivent acquérir ?

Les capacités et dispositions

J’ai lu plusieurs fois dans des ouvrages écrits par des spécialistes en sciences de l’éducation en en neurosciences que le fait d’être convaincu d’être capable d’apprendre quelque chose est déterminant pour la réussite de l’apprentissage, et qu’en conséquence il faut convaincre les élèves qu’iels sont parfaitement capables d’atteindre les objectifs des enseignements qu’iels suivent.

Mais en constatant l’extrême difficulté de certaines personnes pourtant motivées à maîtriser des sujets que d’autres dominent avec une rapidité intimidante, je me demande s’il faut vraiment encourager les premières à s’acharner, plutôt que de leur conseiller un changement d’orientation.

J’ai l’impression que tout le monde n’a pas les mêmes dispositions – à un âge donné – pour l’étude de toutes les disciplines ni pour l’acquisition de toutes les compétences. Si un ou une de mes élèves a de très grosses difficultés en programmation (codage), j’hésite à l’encourager à continuer dans ce domaine parce que je crains que même si iel réussit à obtenir les certifications visées, iel se retrouvera en situation professionnelle avec des collègues qui auront toujours une longueur d’avance et une plus grande aisance, voire une certaine virtuosité.

Si, en apprenant à conduire une automobile, vous avez plusieurs accidents, qu’il vous faut beaucoup plus de temps que la plupart des gens pour maîtriser le véhicule, que vous êtes encore angoissé de prendre le volant après des centaines d’heures de pratique, vous pouvez quand même, à force d’efforts et de persévérance, obtenir le permis et devenir un conducteur apte à prendre la route au quotidien. Mais est-ce raisonnable de choisir une orientation professionnelle vers le métier de conducteur d’ambulance ?

J’ai deux hantises contradictoires :

1. Dire une personne apprenante : « Ayez confiance en vous, tout le monde peut y arriver, c’est juste une question de temps, de pratique, de méthode, persévérez, allez-y ! » et constater que cette personne double ou triple des années de formation, finit par valider de justesse en 7 an un parcours prévu pour être réalisé en 3 ans, sans vraiment dominer son sujet.
2. Conseiller à une personne de changer d’orientation alors qu’elle aurait peut être pu réussir à devenir très compétente dans le métier de ses rêves.

Apprendre sans comprendre

Je me rappelle avoir passé des centaines d’heures, si ce n’est des milliers, au cours de mon parcours scolaire et universitaire à écouter et recopier des choses dont je ne comprenais pas le sens. Peut-il y avoir un bénéfice d’apprentissage à reproduire, notamment par écrit, des connaissances qu’on ne comprend pas ? Entendez pas là, Y-a-t-il des situations où reproduire sans comprendre pourrait être une approche d’apprentissage plus efficace qu’aller plus lentement pour se donner le temps de décrypter, analyser et comprendre ?

Le plaisir d’apprendre

Peut-on se forcer à apprendre efficacement quelque-chose qui nous barbe profondément ?

---