Ai-je compris tous les messages de la vidéo Marilyn versus Monty Hall | Bayes 4 diffusée sur l’excellente chaîne Science4All, animée par le mathématicien Lê Nguyên Hoang ? Cette vidéo aborde un problème éponyme de probabilités conditionnelles dans lequel un participant d’un jeu télévisé doit choisir un rideau parmi trois, sachant que derrière un des rideaux se cache une voiture et derrière chacun des deux autres une chèvre. Après son premier choix, le candidat reçoit une nouvelle information qui est la localisation d’un rideau, parmi les deux qu’il n’a pas choisi, derrière lequel se trouve une chèvre. La question posée est : sur la base de cette nouvelle information, le candidat a-il intérêt à modifier son choix initial ?

La première partie de la vidéo est très intéressante et je vous invite à la regarder car elle montre que même des mathématiciens expérimentés peuvent faire des erreurs de raisonnement. Dans la deuxième partie, qui commence à 10:45, Lê explique comment utiliser la formule de Bayes pour résoudre le problème des trois rideaux. Je vais reprendre son explication avec un regard critique en tentant d’apporter quelques éléments qui, je pense, m’auraient permis comprendre plus vite la démarche proposée s’ils avaient été donnés dans la vidéo.

Tout d’abord, je vais rappeler la version la plus simple de la formule de Bayes, et je donnerai ensuite la version utilisée par Lê. La première version fait intervenir deux variables H et D qui représentent des ensembles d’observations possibles auxquelles sont associées des probabilités. L’ensemble D représente des observations pouvant être faites lors d’une expérience, et l’ensemble H les observations qui sont cohérentes avec une certaine hypothèse. On se permettra d’utiliser la même notation H pour désigner l’hypothèse et les évènements observables en cohérence avec cette hypothèse. Voici une figure illustrant cette première variante de la formule de Bayes.

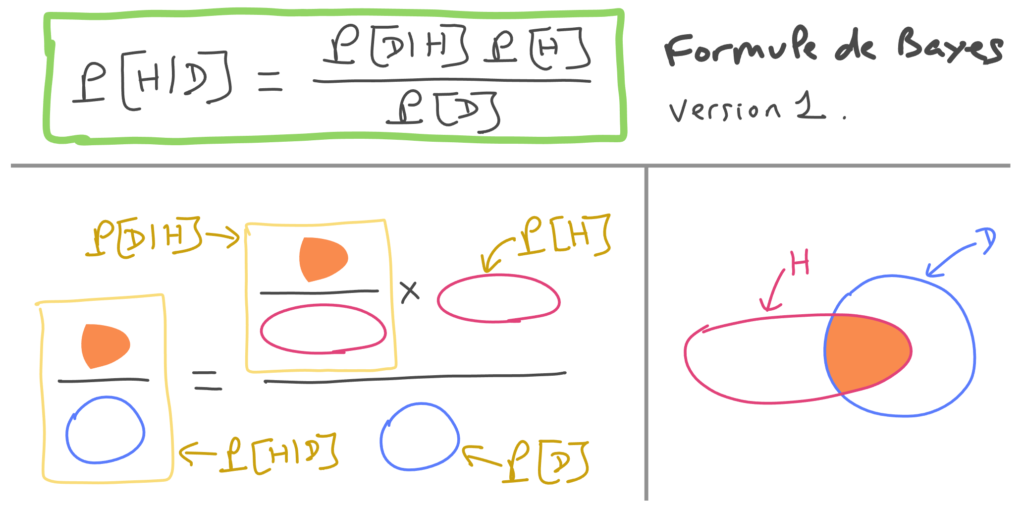
La figure ne couvre pas tous les cas possibles. Il se pourrait par exemple que D soit inclus dans H, ou que H soit inclus dans D, mais la formule, elle, s’applique dans tous les cas. Elle exprime la probabilité qu’une observation soit cohérente avec l’hypothèse H sachant que cette observation est dans D, et fait intervenir les probabilités suivantes :

• La probabilité P[D|H] qu’une donnée observée soit dans D sachant que cette donnée est cohérente avec H.
• La probabilité P[H] qu’une observation soit cohérente avec H.
• La probabilité P[D] qu’une observation soit dans D.

Dans la vidéo, Lê parle de théorie plutôt que d’hypothèse, et utilise la lettre T pour désigner cette théorie. Mais dans les deux cas, je pense qu’on parle bien d’un ensemble d’observations possibles ayant chacune une certaine probabilité. D’autre part, il utilise une version de la formule de Bayes dans laquelle la probabilité P[D] est décomposée sous la forme d’une somme dans laquelle apparaissent les probabilités conditionnelles d’observer une donnée de type D selon différentes théories. On considère alors implicitement un ensemble d’hypothèses (théories) qui contient une hypothèse H à laquelle on s’intéresse particulièrement, mais aussi les autres hypothèses alternatives. Voici la manière dont Lê écrit la formule. La lettre T désigne l’hypothèse à laquelle on s’intéresse, et la lettre A désigne les hypothèses alternatives.

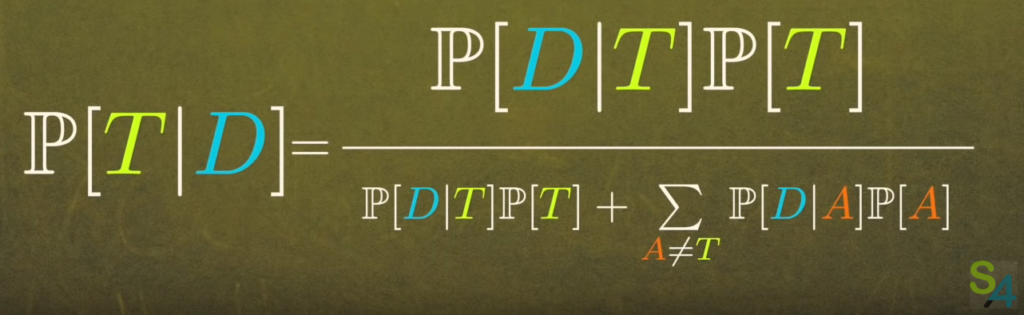
Voici une reformulation de la décomposition qui apparait au dénominateur. J’ai utilisé les lettres A et H pour désigner respectivement l’hypothèse de référence et les hypothèses alternatives, et un H majuscule cursif pour désigner l’ensemble de toutes les hypothèses (i.e. l’hypothèse de référence et les hypothèses alternatives).

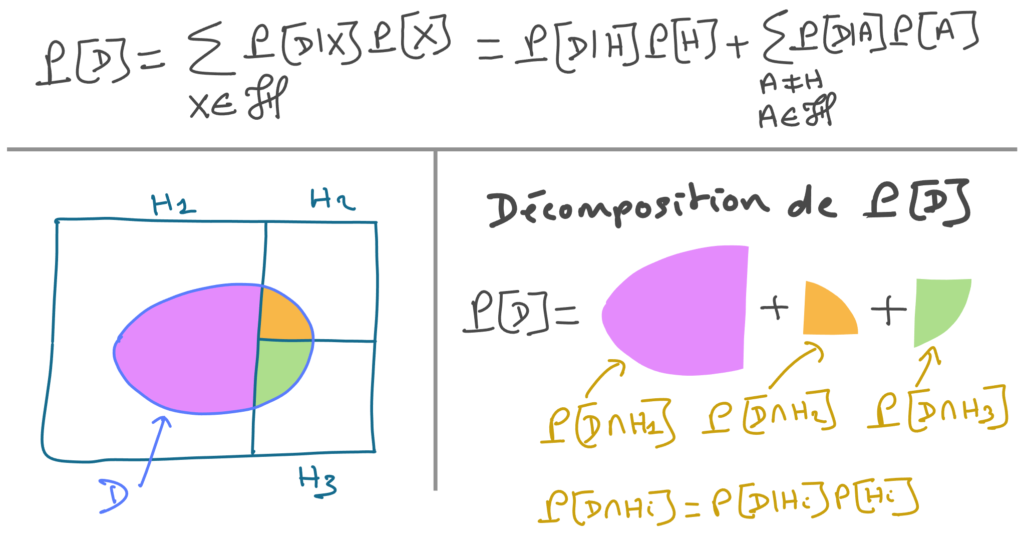
Mais attention ! Il y a quelque chose que Lê ne précise pas et qui me parait important : La décomposition de P[D] n’est correcte que si les hypothèses considérées sont mutuellement exclusives et couvrent toutes les observations possibles. En d’autres termes, chaque observation possible doit être cohérente avec une hypothèse et une seule. Il est facile de voir sur la figure ci dessus que si par exemple H2 et H3 se recouvrent, ça ne fonctionne plus.

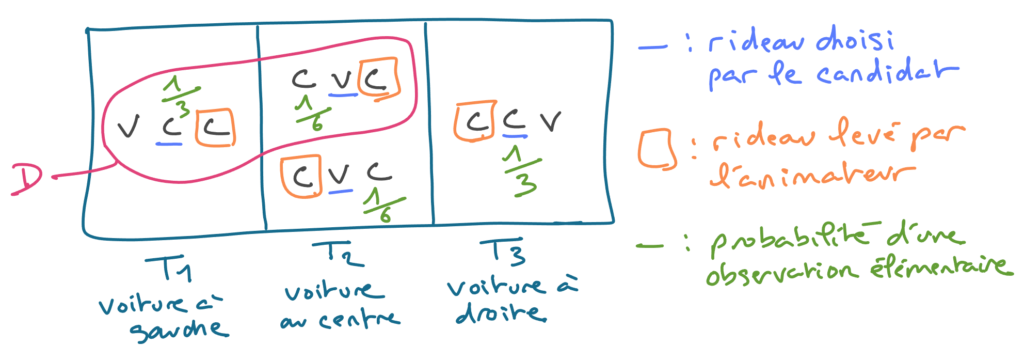
Rentrons maintenant dans le vif du sujet. Lê introduit trois hypothèses (théories) correspondant aux trois emplacements possibles de la voiture. Il attribue la probabilité 1/3 à chacune de ces hypothèses, ce qui me parait raisonnable puisqu’on a aucune information et qu’on peut même supposer que cet emplacement a été choisi aléatoirement. Il appelle préjugé ces trois probabilités. Sans perte de généralité, il suppose que le candidat a choisi le rideau du milieu, puis se place dans le cas où le présentateur a révélé qu’une chèvre se trouvait derrière le rideau de droite. Au regard de cette information, Lê calcule les probabilités de la donnée observée D = [il y a une chèvre à droite] pour chacune des des trois théories, à savoir T1 : la voiture est à gauche, T2 : la voiture est au milieu, et T3 : la voiture est à droite. Sauf qu’il ne numérote pas explicitement les théories et utilise à chaque fois la lettre T. Je pense que le raisonnement aurait été plus facile à suivre avec une numérotation des trois hypothèses.

Quoi qu’il en soit, on a P[D|T3] = 0 parce que sous l’hypothèse T3 où la voiture est à droite, la probabilité d’observer une chèvre à droite est nulle. Ce terme P[D|T3] est appelé terme d’expérience de pensée de la théorie T3. Ensuite, on a P[D|T1] = 1 car sous l’hypothèse T1 où la voiture est à gauche, le présentateur ouvre forcément le rideau de droite (puisqu’il ne veut pas montrer la voiture ni lever le rideau initialement désigné par le candidat). Enfin P[D|T2] = 1/2 car sous l’hypothèse T2 où la voiture est au milieu, le présentateur peut choisir de révéler soit la chèvre de droite, soit la chèvre de gauche. Lê traduit cela par la phrase « Dans la théorie T2, on prédit la donnée observée avec probabilité 1/2 ».

Ensuite, Lê calcule le score de chaque théorie, c’est à dire les termes P[D|T1] P[T1] = 1/3, P[D|T2] P[T2] = 1/6 et P[D|T3] P[T3] = 0. On perçoit ici qu’au regard de l’information D dont on dispose, la théorie T1 (la voiture est à gauche) est deux fois plus probable que la théorie T2 (la voiture est au milieu). On applique alors la formule de Bayes pour chacune des trois théories. Lê fait un raccourci en s’appuyant implicitement sur le fait que les trois théories sont équiprobables. Sans ce raccourci, le dénominateur vaut 1x(1/3) + (1/2)x(1/3) + 0x(1/3) = 1/2. Les probabilités des trois théories sachant la donnée connue sont respectivement P[T1|D] = 2/3, P[T2|D] = 1/3 et P[T3|D] = 0. Donc le candidat a deux fois plus de chance de gagner la voiture s’il change d’avis et choisi le rideau de gauche.

La question importante que Lê n’aborde pas, peut être parce qu’il trouve la réponse évidente, c’est l’utilité de la décomposition de la probabilité P[D]. Aurait-on pu calculer facilement cette probabilité et utiliser directement la première variante de la formule de Bayes ? J’ai l’impression que la réponses est non. Il est difficile d’appréhender cette probabilité que l’animateur révèle une chèvre derrière le rideau de droite sans prendre en compte les différentes théories T1, T2 et T3 et cela méritait d’être dit. Une autre petite critique est qu’il est difficile de bien se représenter ce que sont les observations élémentaires pouvant appartenir aux ensembles T1, T2, T3 et D, et un effort explicatif aurait pu être fait à ce niveau. Si j’ai bien compris, une observation combine deux informations : la position de la voiture et le rideau levé par l’animateur. Voici une illustration graphique qui montre ce que je considère être les 4 observations possibles (de probabilités non nulles) si le candidat choisit initialement le rideau du milieu. Chacune de ces observations inclut tout l’historique, depuis la position de la voiture et des chèvres jusqu’au rideau levé par l’animateur. On voit notamment que P[D] vaut 1/3 + 1/6 = 1/2.

Pour conclure, ma principale critique de la vidéo objet de ce billet, c’est qu’il manque une explication de la nature des objets mathématiques représentés par les lettres T (théorie) et D (donnée connue ou observée). A tel point que j’espère ne pas m’être fourvoyé en considérant que T (ou les Ti) et D sont des ensembles d’évènements élémentaires, chacun pouvant être observés avec une certaine probabilité. Mais si je me suis trompé, j’espère que l’auteur passera par là et pourra apporter des précisions qui me permettront de modifier ce billet.

Concernant le choix de ce problème particulier pour illustrer la puissance de la formule de Bayes, je dirais que le caractère contrintuitif de la solution et le fait que le problème soit célèbre sont des facteurs positifs. Mais par contre, le fait que les « possibles » soit des objets assez complexes, incluant la position de la voiture et le rideau levé par l’animateur, fait qu’il me serait assez difficile de faire le raisonnement « Bayésien » sans être guidé par un spécialiste. En outre, il y a un raisonnement très simple et pas spécialement Bayésien qui permet de conclure de manière convaincante, en imaginant qu’il y a deux candidats, Anne et Barnabé.

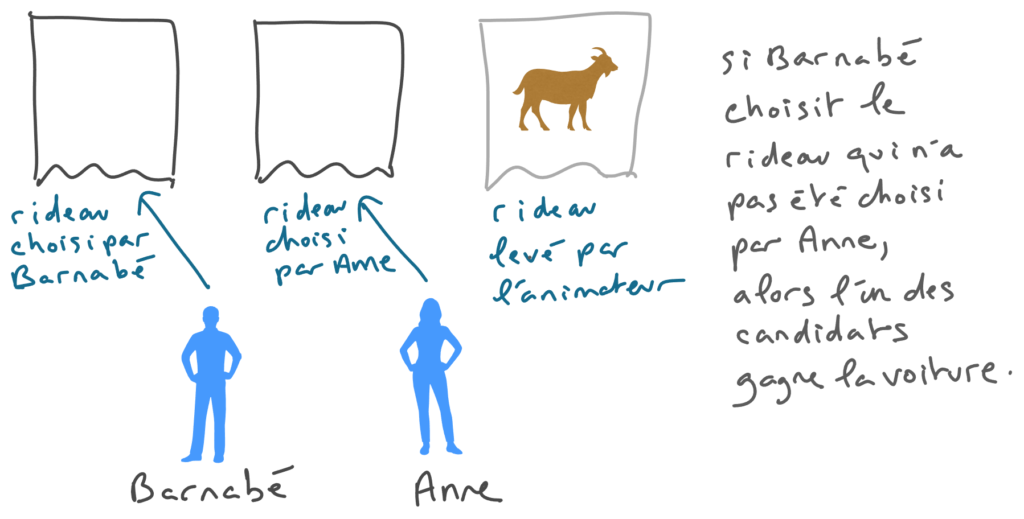
Anne joue en premier et choisi le rideau central. Elle ne change pas d’avis. Puis le présentateur dévoile une chèvre, et ensuite Barnabé choisi le rideau restant qui n’a pas été choisi par Anne. Clairement, l’un des deux candidats gagne la voiture. Comme la voiture a une probabilité 1/3 d’être remportée par Anne, alors elle a une probabilité 2/3 d’être gagnée par Barnabé.

Lê anticipe cette critique en disant que le but de la vidéo n’est pas spécifiquement de monter la manière la plus simple de résoudre le problème donné en exemple, mais de montrer comment le résoudre de manière « Bayésienne ». Mais il reste qu’il y a un gouffre entre la simplicité de la résolution de ce problème avec Anne et Barnabé et la relative complexité de sa résolution avec Bayes.