Ce que je vais dire ici à propos des mathématiques correspond à l’état actuel de ma compréhension des fondements de ce domaine, et résulte de centaines d’heures de réflexion réparties tout au long de ma vie. Ma compréhension évolue en permanence. Si vous êtes mathématicienne ou mathématicien et que certains de mes propos vous paraissent erronés, merci de me le signaler, par exemple en m’écrivant à olivier point bailleux at u tiret bourgogne point fr.

Les mathématiques, c’est quoi ?

En l’état actuel de ma compréhension (je suis une personne de 58 ans, docteur en informatique, habilité à diriger des recherches, enseignant chercheur universitaire en informatique), la science mathématique s’intéresse à deux sortes d’objets :

• des objets purement syntaxiques, constitués de suites de symboles pouvant être écrites par exemple sur papier ou écran,
• des objets immatériels, abstraits, tels que des nombres, des ensembles, des relations, des fonctions, des injections, des surjections, des espaces vectoriels, des structures algébriques, des groupes, des morphismes, etc. etc. etc.

Les objets mathématiques abstraits peuvent être nommés, identifiés, voire représentés par des expressions écrites en langage mathématique. Toutefois, les représentations d’objets mathématiques abstraits en langage mathématique ne sont généralement pas des objets mathématiques purement syntaxiques. Cette nuance est extrêmement difficile à comprendre. Il m’a fallu des décennies pour la saisir et je ne suis pas certain de l’avoir complètement cernée.

Par exemple :

• La notation $\mathbb{N}$ n’est pas en elle-même un objet mathématique. C’est la désignation standard de l’ensemble des entiers naturels, qui est un objet mathématique abstrait.
• L’expression $s(s(z))$ peut être considéré comme un objet mathématique purement syntaxique, dès lors que les symboles $s$ et $z$ n’ont pas de sens standardisé dans le contexte où on les utilise.
• En revanche, si $s$ désigne la fonction de $\mathbb{N}$ dans $\mathbb{N}$ qui à tout $x$ associe son successeur, et si $z$ désigne l’entier 0, alors cette même expression $s(s(z))$ est une représentation de l’entier naturel généralement désigné par le symbole 2. On peut dire que l’entier 2 est une des interprétations possibles du terme formel, c’est à dire de l’objet mathématique purement syntaxique, $s(s(z))$.

Les mathématiciennes et mathématiciens s’intéressent aux propriétés des objets mathématiques abstraits. Iels expriment ces propriétés avec des énoncés mathématiques. Un tel énoncé est soit vrai, soit faux.

Lorsque ces énoncés expriment des propriétés qui contribuent à spécifier un ou plusieurs objets mathématiques, on les appelle axiomes. Lorsqu’ils expriment des propriétés qui ont été déduites d’un ensemble d’axiomes, on les appelle des théorèmes.

On peut coder les énoncés (donc les axiomes et les théorèmes), mais aussi les déductions et les preuves, avec des objets mathématiques purement syntaxiques, et s’appuyer sur une telle formalisation pour modéliser mathématiquement… le raisonnement mathématique. On « jongle » alors avec plusieurs niveaux d’abstraction.

Par exemple, voici un énoncé exprimé en français :

La somme de deux entiers naturels impairs est toujours un entier naturel pair.

Cet énoncé comporte beaucoup d’information implicite. Pour en saisir le sens, il faut comprendre en profondeur ce qu’est un entier naturel, la somme de deux entiers naturels, un entier naturel pair et un entier naturel impair.

Voici une reformulation plus détaillée :

Pour tout $x \in \mathbb{N}$ et pour tout $y \in \mathbb{N}$, si il existe $t \in \mathbb{N}$ et $u \in \mathbb{N}$ tels que $x = 2t + 1$ et $y = 2u +1$, alors il existe $s \in \mathbb{N}$ tel que $x+y = 2s$.

Dans cette deuxième version, seuls les symboles $x, y, t, u, s$, appelés variables, sont des objets mathématiques purement syntaxiques ayant une infinité d’interprétations. Chacune de ces interprétations met en relation chaque variable avec un objet mathématique abstrait. La notation « $\in \mathbb{N}$ » restreint ces interprétations aux entiers naturels. Les autres symboles sont des notations standards désignant chacune un unique objet mathématique abstrait. Par exemple, $+$ désigne une fonction particulière de $\mathbb{N}$ dans $\mathbb{N}$, appelée addition standard, et $=$ désigne la relation identité sur $\mathbb{N}$.

Cet énoncé peut être codé à l’aide d’objets mathématiques purement syntaxiques appartenant au langage arithmétique de Peano, ce qui donne :

$\forall x \forall y$ $($ $\exists u$ $($ $\text{add}(\text{mul}(\text{succ}(\text{succ}(\text{zero}))),u)$ $,$ $\text{succ}(\text{zero})$ $)$ $=$ $x$ $\wedge$ $\exists t$ $($ $\text{add}(\text{mul}(\text{succ}(\text{succ}(\text{zero}))),t)$ $,$ $\text{succ}(\text{zero})$ $)$ $=$ $y$ $)$ $\to$ $($ $\exists s$ $($ $\text{add}(x,y)$ $=$ $\text{mul}(\text{succ}(\text{succ}(\text{zero})),s)$ $)$

Cette troisième version de l’énoncé est un objet mathématique purement syntaxique, qui peut être interprété d’une infinité de façons différentes, bien que certains symboles, comme $\exists$ et $\wedge$, aient une interprétation standard définie dans le cadre de la logique. On peut prouver « mécaniquement » que la propriété encodée est une conséquence logique d’un ensemble d’axiomes qui modélisent la notion de successeur, l’addition et la multiplication d’entiers naturels. Les axiomes de départ restreignent les interprétations des symboles $\text{add}$, $\text{mul}$ et $\text{succ}$.

Typiquement, la démarche de recherche en mathématiques consiste à partir d’axiomes spécifiant certaines propriétés d’objets mathématiques, puis à réaliser des déductions qui aboutissent à des théorèmes qui sont vrais pour tous les objets mathématiques vérifiant les axiomes de départ. On appelle preuve d’un théorème la suite de déductions aboutissant à ce théorème.

Ce n’est qu’au vingtième siècle (à ma connaissance) que la communauté mathématique a réalisé qu’en considérant les énoncés, déductions et preuves comme des objets mathématiques à part entière, on pouvait mettre en abîme les mathématiques en s’appuyant sur le formalisme de la logique. C’est à dire qu’on pouvait, par exemple, construire des énoncés dont les variables représentent des énoncés, des déductions ou des preuves, et prouver que certaines méthodes de preuves produisent toujours des conséquences logiques des axiomes de départ. C’est à ce moment là que Kurt Gödel a démontré qu’aucun ensemble « exploitable » d’axiomes ne permettait de prouver tous les énoncés vrais formalisant les propriétés arithmétiques, mêmes celles pouvant s’exprimer uniquement avec des additions et multiplications sur les entiers naturels.

Un autre but des mathématiciennes et des mathématiciens est de produire des méthodes de calcul permettant de résoudre certains problèmes de manière efficace et automatisable, ce qui nous amène aux domaines d’utilisation et d’application des mathématiques.

Domaines d’utilisation

Beaucoup de systèmes complexes, dans de nombreux domaines techniques et scientifiques, peuvent être modélisés par des objets mathématiques, ce qui permet, grâce à des calculs, de prévoir leur comportement ou, si applicable, de déterminer les configurations et paramètres permettant d’obtenir un comportement particulier.

Les applications sont multiples, dans les domaines les plus variés tels que la physique, la chimie, l’informatique, l’électronique, la finance, l’économie, les transports, les télécommunications, l’informatique, la biologie, la médecine, la météorologie, l’exploration spatiale, l’architecture, etc.

Toutefois, bien que les mathématiques y aient un rôle crucial , une toute petite proportion des personnes travaillant dans tous ces domaines doivent réellement maîtriser les fondements des concepts et outils mathématiques qui y sont utilisés. Les autres personnes exploitent, dans le cadre de leurs activités professionnelles, des formules, des abaques, des applications ou des procédures standardisées qui ne requièrent pas de maîtriser la théorie sous-jacente.

De fait, une très grande partie des savoirs mathématiques abordés lors des cursus scolaires et d’enseignement supérieur ne seront pas utilisés dans un contexte professionnel par la plupart des personnes ayant suivis ces cursus. Ceci n’implique pas que l’enseignement de ces savoirs soit inutile, mais simplement que, pour la plupart des gens, l’utilité de ces enseignements, si applicable, est ailleurs.

Par exemple, je découvre (je l’avoue, avec une certaine stupéfaction) au moment où j’écris ces lignes que l’étude des polynômes de degré 3 (tableau de variation, extremums, nombre de solutions…) est au programme de toutes les classes de terminales de bac professionnel. Il est parfaitement clair que, sauf extraordinaire exception, aucun paysagiste, mécanicien automobile, gérant de commerce ou de restaurant n’aura à mettre en application de telles connaissances dans le cadre de son activité professionnelle. Pour ces personnes, l’utilité d’un tel savoir, si applicable, ne peut être qu’indirecte.

Dans le même programme commun à tous les bac pro, « le calcul du terme de rang donné d’une suite arithmétique dont le premier terme et la raison sont donnés » doit faire l’objet d’un entraînement régulier, sous forme « d’activités rituelles » jusqu’à devenir un automatisme. Si cet objectif semble largement atteignable par une très grande majorité des élèves concernés, il me parait excessivement peu probable que ces personnes aient l’occasion d’exploiter un tel automatisme dans le cadre de leur futur métier. Encore une foi, il faut chercher ailleurs l’utilité d’un tel enseignement. Je reviendrai sur ce point à la fin de ce billet.

Petite anecdote, au moment ou j’ai écris le paragraphe précédent, je n’avais pas en tête un quelconque automatisme permettant de calculer le terme de rang donné d’une suite arithmétique dont le premier terme et la raison sont donnés. Je n’ai d’ailleurs jamais participé à des rituels destinés à automatiser ce genre de calcul. Toutefois, j’ai trouvé la solution en moins d’une minute, avec une simple feuille de brouillon et un crayon.

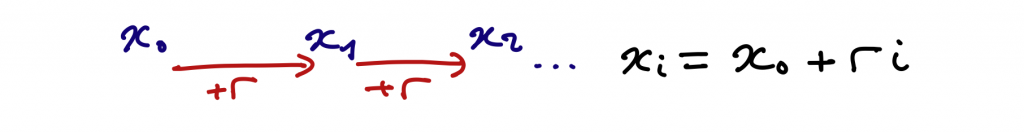
J’ai retrouvé la définition d’une suite arithmétique en réactivant une connaissance ancienne, mais j’ai construit la formule par la réflexion, car à l’époque où la notion avait été abordée dans mon cursus scolaire, ce genre de chose me barbait tellement que je n’avais même pas essayé de la retenir.

Utilisations dans la vie quotidienne

Je vous propose une petite expérience. Essayez de vous rappeler et de recenser les occasions d’utilisation des mathématiques votre vie quotidienne, hors vie professionnelle, hors assistance aux devoirs d’enfants scolarisés ou personnes suivant une formation, et hors loisirs mathématiques ou mathématiques récréatives.

Je me prête au jeu et j’obtiens la liste suivante, non exhaustive mais, je pense, assez représentative.

• Je fais régulièrement appel à ma compréhension de la notion de proportionnalité, notamment pour calculer des pourcentages me permettant de comparer des proportions.
• J’utilise des additions et soustractions pour gérer mes comptes bancaires et mon budget.
• Je fais des calculs combinatoires pour déterminer le niveau de sécurité d’un code secret, d’un cadenas à chiffres, d’un mot de passe…
• J’utilise la notion de rapport, ou quotient, pour comparer des ordres de grandeurs, par exemple dans le domaine de la consommation d’énergie lors des activité quotidiennes (chauffage, eau chaude, déplacements…)
• Les notions d’aire, de multiplication et de racine carrée m’ont permis de mieux visualiser ce que représentent les 8000 hectares de forêt décimés par un incendie dans une région de France.
• Les fonctions puissances et les suites géométriques me permettent de mieux appréhender la notion de croissance exponentielle qui intervient notamment dans certaines phases des épidémies.
• Les fonctions affines par morceaux me permettent de comprendre comment est calculé mon impôt sur le revenu et pourquoi je ne peux pas perdre d’argent en changeant de tranche d’imposition.
• La composition multiplicative de plusieurs facteurs et la notion de probabilité me permettent de comparer les risques de transmission du virus de la CoVid selon le contexte et les précautions prises, et notamment le lien entre ce risque et la concentration de CO2 en intérieur.
• La notion de probabilité conditionnelle me permet d’avoir un regard nuancé sur certains phénomènes de société, par exemple en faisant bien la distinction entre la proportion d’hommes parmi les personnes emprisonnées et la proportion de personne purgeant une peine de prison parmi celles appartenant à la gent masculine.
• Mes quelques connaissances en statistiques et probabilités me permettent de comprendre qu’être témoin d’un évènement, et à fortiori être informé par la presse d’un évènement, n’implique pas que cet évènement soit probable, et qu’inversement, ne jamais avoir été témoins d’un évènement n’implique pas qu’il soit très improbable. D’une manière générale, mes connaissances en probabilités et statistiques, bien que limitées, me permettent de prendre du recul vis à vis des informations données par la presse et des affirmations (parfois mensongères) vues sur les réseaux sociaux ou entendues dans mon entourage.
• Le raisonnement logique m’est utile quotidiennement, pour toutes mes réflexions.

Il ressort de cette liste deux choses remarquables.

1. Une partie des notions de mathématiques étudiées durant ma scolarité me sont utiles dans la vie quotidienne, bien qu’à un niveau technique nettement inférieur à celui auxquelles ces notions ont été abordées en classe. Je réalise parfois quelques calculs simples, mais c’est surtout une compréhension en profondeur des notions concernées qui m’est utile pour mieux organiser, relier, interpréter les informations que je reçois.
2. Beaucoup de notions de mathématiques étudiées durant ma scolarité ne m’ont jamais été directement utiles dans la vie quotidienne. C’est le cas par exemple de de la continuité, des dérivées et primitives, du calcul intégral, de la trigonométrie, des espaces vectoriels, de l’analyse de fonctions continues, des nombres complexes, des techniques de calcul de convergence de suites numériques…

Les mathématiques à l’école

Pourquoi faut-il enseigner les mathématiques à l’école, au collège, au lycée, et au delà ? Quelles notions doivent-être abordées, quand, et comment, avec quels objectifs ? Ces questions ne sont pas nouvelles. Elles sont même au coeur des préoccupations de millions de décideuses, décideurs, enseignantes, enseignants, entrepreneuses, entrepreneurs, et autres personnes. Mais les réponses apportées me laissent parfois un peu perplexe. Voici l’état actuel de mes réflexions, en tant qu’ancien élève, qu’enseignant universitaire et que citoyen.

1 – Kit de survie

Certaines compétences sont indispensables pour faire face aux problèmes et activités de la vie quotidienne comme par exemple comprendre ce qu’est une quantité discrète ou continue, une addition, une multiplication, une proportionnalité, un pourcentage, les unités de longueur, surfaces, volumes, et la capacité à mettre en pratique ces connaissances en réalisant des calculs simples, en utilisant une calculette, et même à la main ou de tête, au moins pour des petites valeurs (inférieures à 100) ou des valeurs arrondies (à deux chiffres significatifs).

Tous les outils mathématiques couramment utilisés dans les activités quotidiennes, telles que faire ses courses, gérer un budget, prévoir les quantités de boisson et nourriture pour une fête d’anniversaire ou une randonnée, détecter une erreur importante sur une facture, doivent évidemment être enseignés dès que possible. Je pense que ce point fait consensus.

2 – Prendre du recul

Certains concepts mathématiques nous permettent de comprendre ou d’améliorer notre compréhension du monde dans lequel nous vivons et peuvent nous aider à prendre des décisions et à nous forger des opinions. Je pense notamment aux probabilités et statistiques, aux probabilités conditionnelles, aux fonctions puissances, linéaires, polynomiales, logarithmes, au calcul combinatoire. Certaines bases mathématiques, notamment, son nécessaires pour assimiler des notions de physique, par exemple liée aux concepts de puissance et d’énergie, qui ont une importance considérable dans notre quotidien.

J’estime nécessaire que ces notions soient enseignées à toutes et à tous, pas dans le but de créer des automatismes, ni de permettre aux gens de réaliser des calculs complexes, mais plus dans un esprit de vulgarisation scientifique.

3 – Apprendre à penser

Je pense qu’il s’agit d’un rôle crucial de l’enseignement des mathématiques : amener les élèves à développer leurs capacités de déduction, d’analyse, de généralisation, d’abstraction, leur capacité à exploiter des techniques, des outils, des principes connus pour résoudre des problèmes qu’iels n’ont encore jamais rencontré, et à cultiver leur curiosité et leur exigence et leur rigueur intellectuelles.

Ces qualités et compétences permettent, tout au long de la vie, d’atteindre des objectifs ambitieux et gratifiants, comme réussir des études supérieures, accéder à des métiers intéressants et à des postes bien rémunérés (ou pas !), contribuer à l’amélioration des conditions de vie des gens…

Sauf que l’idée que nos capacités à résoudre des problèmes mathématiques sont transférables à d’autres domaines pourrait-être un neuromythe. Je cite un tweet de Jean-François Parmentier, chercheur associé sur le numérique pour l’éducation à l’IRIT Toulouse, que j’ai lu après avoir écrit ce billet :

…enseigner les maths apprend à être rigoureux… en math ! Et pas à acquérir un compétence magique de « rigueur de raisonnement ». Il n’y a PAS de transfert entre savoir raisonner dans un domaine (échec, math, latin, …) et savoir raisonner dans un autre domaine.

4 – Outils pour d’autres matières

Certains outils mathématiques sont des prérequis pour les objectifs d’enseignement d’autres disciplines, comme par exemple la physique, la chimie, la biologie, la géographie, l’économie.

5 – Acquérir des compétences professionnelles

Bien évidemment, dans les formations professionnelles à des métiers qui utilisent des outils mathématiques (modélisation, calcul), il est indispensable de transmettre aux élèves les compétences liées à l’utilisation de ces outils.

6 – Développer les talents

Tout le monde n’a pas vocation à devenir mathématicienne ou mathématicien, ni à s’orienter vers des domaines nécessitant un niveau élevé en mathématiques. Mais on peut penser que la découverte des mathématiques dès l’enfance, ou l’intérêt suscité par cette matière lors de l’adolescence, peut permettre à certaines personnes de prendre conscience de leur potentiel et les amener à choisir une voie à laquelle elles n’auraient pas songé si elle n’avaient pas eu l’occasion de découvrir certains aspects des mathématiques lors de leur scolarité.

7 – Culture scientifique

Les mathématiques font partie du patrimoine immatériel de l’humanité, au même titre que les grandes oeuvres littéraires, musicales, et de tous les autres domaines de la connaissance. À ce titre, de nombreux éléments de mathématiques devraient être considérés comme appartenant à la culture générale. Je pense, par exemple, au théorème de Pythagore, à certains ensembles de nombres tels que les naturels, les réels, les rationnels, les irrationnels, les complexes, au nombre Pi, à la trigonométrie, à ce qui touche à la notion d’infini et d’ensembles dénombrables ou non dénombrables, ou encore à la démarche axiomatique. Une telle culture peut s’acquérir tout au long de la vie et être très différente d’une personne à l’autre. Il ne faut pas confondre culture générale et culture universelle. Dans le cadre scolaire, elle pourrait être abordée, à tous niveaux, dans des enseignements d’histoire des sciences.

Mon regard sur les objectifs

J’en arrive à la conclusion qu’il y a de très bonnes raisons d’enseigner les mathématiques à tout le monde, en différenciant toutefois les objectifs d’apprentissage à partir d’un certain stade. C’est précisément ce que fait notre système éducatif. Mais il me semble très important de ne pas se tromper d’objectif, et d’utiliser des approches pédagogiques à la fois adaptées au public concerné et alignées avec les objectifs ciblés.

Il me semble essentiel d’enseigner et de consolider au fil des années les notions mathématiques nécessaires aux deux premiers objectifs présentés plus haut : acquérir des compétences de survie et appuyer notre compréhension du monde dans lequel nous vivons. Par exemple, les notions de probabilités, de statistiques, de proportionnalité, ou encore de croissance exponentielle, linéaire ou polynomiale, devraient être abordées et consolidées à différentes étapes des parcours scolaires, dans l’esprit de les rendre accessibles et compréhensibles par le public ciblé, sur la base d’exemples concrets.

Concernant le troisième objectif, apprendre à penser, [Attention, cet objectif est peut-être illusoire, voir plus haut] ce qui me semble important, ce ne sont pas tant les notions mathématiques abordées – elles doivent être multiples et diverses – que la manière des les aborder et le moment où elles sont abordées, c’est à dire le quand et le comment.

Concernant le quatrième et le cinquième objectifs, acquérir des compétences métiers et maîtriser des outils nécessaires pour progresser dans d’autres disciplines, il me parait important de bien distinguer :

• d’une part, les outils mathématiques indispensables,
• et d’autre part, les fondements théoriques de ces outils, qui relèvent de la culture scientifique et qui, je pense, ne devraient pas avoir de caractère éliminatoire dans les évaluations et certifications.

Le sixième objectif, susciter des vocations et détecter des talents, est très important, mais ne devrait pas conduire à imposer à tout le monde des activités perçues comme contraignantes et rébarbatives par certaines personnes. Je pense qu’il faut aborder cet objectif de manière ludique, sans obligation de résultat, et donc sans pénaliser par de mauvaises notes les personnes qui ne s’avèrent pas intéressées, malgré les incitations, par les spécialités qu’on leur fait découvrir.

Quant au septième objectif, la culture scientifique, il devrait, à mon sens, privilégier des approches pédagogiques qui développent la curiosité intellectuelle, sans forcer les choses trop tôt, à un moment ou le public ciblé n’aurait pas la maturité nécessaire pour s’intéresser aux sujets abordés (j’ai constaté que cela ne se produit au même âge pour tout le monde). On ne peut pas amener les gens à s’intéresser à quelque chose à marche forcée.

Mes inquiétudes

J’ai trois motifs d’inquiétude, qui concernent

1. les contenus des programmes, c’est à dire le quoi,
2. les pratiques d’enseignement, c’est à dire le comment, et
3. le moment où sont abordées certaines notions, c’est à dire le quand.

Le quoi

Lorsque je parcoure les programmes scolaires de collège et de lycée, j’ai vraiment le sentiment qu’ils sont très chargés, qu’ils abordent un nombre considérable de concepts issus de milliers d’années de réflexions menées par des personnes brillantes. Pour les élèves ayant une certaine appétence pour les mathématiques, il y a sans nul doute de quoi se régaler. Mais je crains que pour beaucoup de gens, cela provoque un effet de saturation qui entraîne un rejet des mathématiques parfois lourd de conséquences en termes de poursuite d’études et de perspectives professionnelles.

Par ailleurs, il me semble que certains aspects des mathématiques, comme par exemple les études de fonctions, la dérivation, l’intégration, sont sur-représentés dans l’enseignement secondaire général et professionnel, au regard de ce qu’ils apportent aux différents objectifs évoqués plus haut.

Le comment

Les approches pédagogiques préconisées dans les documents officiels et par certains experts en sciences de l’éducation donnent une très grande importance à l’acquisition d’automatismes. Il est évident, et démontré, que l’acquisition d’automatismes est indispensable pour être en mesure de réaliser efficacement des tâches complexes, mais aussi pour apprendre efficacement de nouveaux savoirs. Si une procédure complexe nécessite d’enchaîner des procédures plus simples, et que vous devez mobiliser votre mémoire de travail en tâtonnant laborieusement pour réaliser ces procédures simples, vous êtes en surcharge cognitive et vous perdez le fil de la procédure complexe, ce qui entrave votre apprentissage.

Mais l’acquisition de ces automatismes ne doit pas occulter les objectifs de haut niveau tels que la capacité à analyser une situation nouvelle, à comprendre en profondeur un système complexe, à résoudre un problème nouveau en utilisant à bon escient des approches et techniques antérieurement exploitées dans des contextes différents, à créer une procédure permettant de résoudre une série de problèmes similaires. Je pense qu’imposer aux élèves de graver un automatisme dans leur cerveau représente une grosse responsabilité et doit pouvoir être justifié : à qui cet automatisme sera utile ? Dans quels contextes, quelles circonstances ? Pour quels types de tâches ? À quels moments de la vie ?

Prenons un exemple. Dans certaines classes de collège, l’un des nombreux automatismes à acquérir est de déterminer si un triangle est rectangle, étant données les longueurs de ses cotés, en utilisant la réciproque du théorème de Pythagore. Le problème me parait intéressant comme sujet de réflexion. Mais est-ce raisonnable de l’ériger au statut d’automatisme, c’est à dire d’imposer aux élèves d’être en mesure de le traiter sans réfléchir, de manière immédiate et mécanique ? A mon sens, le principal intérêt d’un tel problème c’est, au contraire, d’essayer de le résoudre en recherchant soi-même une méthode. D’un autre coté, même dans une classe très hétérogène avec de grandes différences de niveaux et de bagages, la plupart des élèves peuvent, avec quelques efforts, maîtriser ce type d’objectif. Cela permet de donner de bonnes notes et peut-être de susciter l’engagement, ou à tout le moins de réduire le découragement. Mais n’y a t-il pas un risque de masquer les difficultés de certaines personnes à progresser vers des compétences cognitives de haut niveau, au lieu de les cibler pour aider chaque élève de développer au mieux son potentiel ?

Dans l’exercice de mon métier d’enseignant universitaire, je constate que certaines personnes apprenantes sont, malgré leur efforts, bloquées dans leurs apprentissages de compétences de hauts niveaux cognitifs relevant du domaine de l’ingénierie. Ces personnes semblent être à la recherche d’automatisme, de « recettes », face à des problèmes qui présentent trop de variabilité pour être traités avec ce genre d’approche. J’ai l’impression qu’il y a eu, au collège ou au lycée, des occasions manquées d’amener ces personnes à mieux développer les compétences que j’ai énoncées plus haut en présentant l’objectif « apprendre à penser ». Bien que leurs aptitudes à déduire, généraliser, analyser, comprendre, et créer soient sans doute intactes, ces personnes ne parviennent pas à les mobiliser au niveau nécessaire, et se retrouvent en situation d’échec.

Le quand

Je crains que certaines notions soient abordées trop tôt pour certains et certaines élèves, c’est à dire à un moment où ces personnes ne maîtrisent pas les prérequis. Cela me parait inévitable dans tout système éducatif où toutes les personnes d’un même âge, quel que soit leur niveau et leurs acquis, ont les mêmes objectifs d’apprentissage et étudient dans les mêmes conditions et au même rythme. L’école de la république ne permet pas de choisir son quand.

Mais les prérequis ne sont pas le seul facteur à considérer. Il y a aussi la maturité intellectuelle des personnes apprenantes. Certaines notions de mathématiques introduites au collège et au lycée m’ont largement échappées parce qu’à l’époque, elles me barbaient profondément et que je n’étais pas motivé pour les apprendre, alors que, quelques années plus tard, elles auraient pu m’intéresser. Tout le monde apprend peut-être de la même manière, mais tout le monde n’est pas intéressé ou motivé, au même âge, par les mêmes choses.

---