Après un test écrit d’entraînement, un enseignant mélange les copies et les redistribue à ses étudiants pour que chacun d’eux corrige le test d’un autre. Mais il peut arriver qu’un étudiant se retrouve avec sa propre copie. Si cette opération était répétée de nombreuses fois, combien d’étudiants, en moyenne, seraient dans ce cas ?

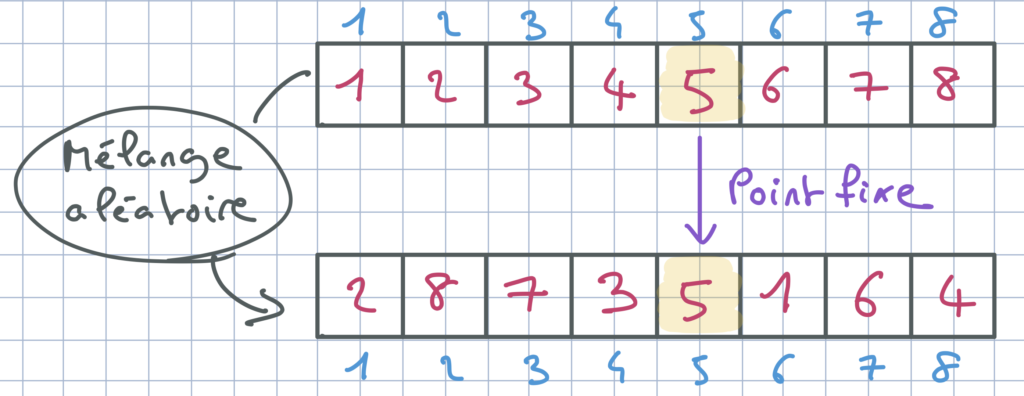
Dans le langage mathématique, le « mélange » des copies s’appelle une permutation, et lorsqu’un des objets mélangés revient à sa place initiale, on appelle cela un point fixe. Or le nombre moyen de points fixes, pour une permutation aléatoire, ne dépend pas du nombre d’objets permutés. (Le nombre de copies, dans notre exemple.) Il est égal à 1. Voici l’explication.

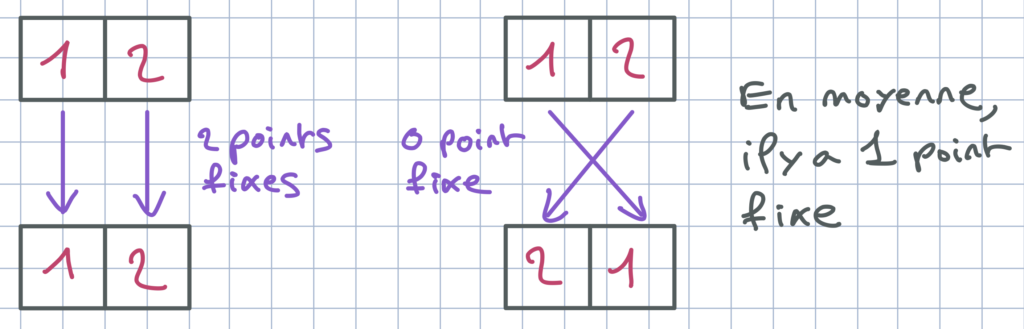
Bien sûr, cette valeur 1 n’est qu’une moyenne. Pour une permutation de n objets, le nombre de point fixes peut varier. Par exemple, s’il n’y a que deux étudiants, soit chaque étudiant récupère sa copie, il y a alors 2 points fixes, soit chaque étudiant récupère l’autre copie, il n’y a alors aucun point fixe. En moyenne, un étudiant récupère sa copie, bien qu’en pratique cela n’arrive jamais.

Maintenant, vous vous demandez peut être quelle est la probabilité qu’il n’y ait aucun point fixe. Une permutation sans point fixe est appelée un dérangement. La probabilité qu’une permutation aléatoire soit un dérangement dépend du nombre n d’objets mélangés, mais pour n suffisamment grand, elle est très proche de 1/e, où e est la base des logarithmes népériens, ce qui fait environ 0,37.