Je travaille actuellement, sur mon temps libre, à la réalisation d’une machine de Turing. Il s’agit d’un ordinateur rudimentaire mais qui permet de réaliser (sous réserve de disposer des ressources suffisantes) tous les calculs que peuvent effectuer les ordinateurs existants, et même ceux qui n’existent pas encore (*), y compris les ordinateurs quantiques. Par contre, cette machine ne calcule pas de manière efficace et n’a donc pas d’intérêt pratique. Alors pourquoi en réaliser une « physiquement » ?

Parce que la machine de Turing occupe une place très importante en science informatique et qu’elle illustre magistralement comment un assemblage d’éléments simples permet de réaliser un système dont le comportement peut être extrêmement complexe au point n’être prévisible, en toute généralité, par aucun algorithme ni aucune machine, aussi compliquée soit-elle. Je pense que le fait de voir une telle machine en fonctionnement peut, plus qu’une simple description ou même une simulation, marquer les esprits de mes étudiants et développer leur curiosité scientifique.

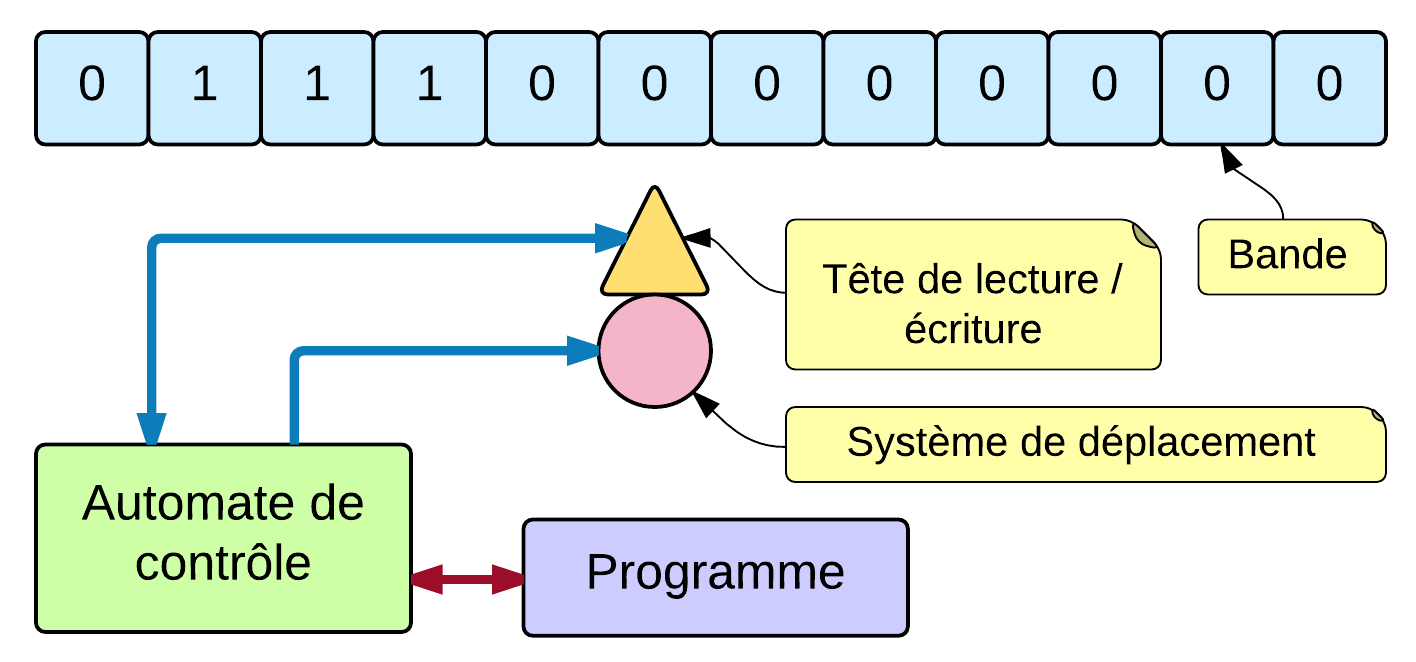
D’autre part, l’analyse de l’architecture et du fonctionnement d’une telle machine montre quels sont les éléments qui la constituent, comment ces éléments échangent des informations, quels sont leurs rôles, comment ils sont eux-mêmes constitués de briques plus simples qui réalisent des opérations élémentaires. Ce genre d’exercice est essentiel pour développer les aptitudes des étudiants en matière d’ingénierie et pour les amener être capables de comprendre et de concevoir par eux-mêmes des systèmes complexes.

Je reviendrai lors d’un prochain billet sur la construction de cette machine. Je dirai juste aujourd’hui qu’elle sera composée de petits modules réalisés avec des composants électroniques simples (portes logiques, bascules D), et que l’état de chacun de ces modules sera indiqué par des leds (bleue pour 0, rouge pour 1) de manière à ce qu’il soit possible de suivre facilement toutes les étapes d’un calcul.

(*) D’après une hypothèse très sérieuse connue sous le nom de thèse de Church-Turing, émise par deux des plus célèbres mathématiciens du siècle dernier.

Faut-il enseigner la programmation à l’école et au collège ? L’idée a souvent été évoquée dans l’actualité de ces derniers mois. En tant qu’universitaire enseignant-chercheur en informatique, je me sens évidemment concerné par cette question.
Je tiens tout d’abord à préciser que le codage (néologisme synonyme de programmation) n’est que la partie technique de la réalisation d’une application. Avant d’arriver à cette étape, il faut avoir une idée, puis créer, à partir de cette idée, une spécification de ce que va réaliser l’application et de la manière dont les utilisateurs vont interagir avec elle. L’utilité, l’attrait et l’utilisabilité d’une application dépendent essentiellement de cette phase de conception qui n’a rien à voir avec le codage. Ce n’est donc pas parce qu’une personne sait coder qu’elle sera capable de réaliser des applications à la fois attractives ou utiles et faciles à utiliser, de la même manière qu’une personne sachant coudre ne sera pas nécessairement douée pour dessiner de nouveaux modèles de robes ou de manteaux, ou qu’un très bon musicien de sera pas nécessairement capable de composer une œuvre musicale à succès.
D’autre part, même si tout un chacun était capable de réaliser ses propres vêtements, très peu de gens utiliseraient effectivement cette compétence. La plupart d’entre eux renouvelleraient leurs garde-robes en allant dans les magasins, et ceci pour une raison très simple : concevoir et fabriquer des vêtements prend énormément de temps. De la même manière, même les gens qui maîtrisent la programmation achètent la plupart des applications dont ils ont besoin car la réalisation d’une application représente souvent des milliers d’heures de travail. Nous vivons dans une société où la plupart des biens de consommation, y compris dans le domaine de l’informatique, sont conçus et fabriqués par des professionnels spécialisés. La grande majorité des gens ne construisent pas leur voiture ni leur maison, ne fabriquent pas eux-mêmes leurs vêtements ni leurs meubles, et n’ont pas plus vocation à réaliser eux-mêmes les logiciels dont ils ont besoin, quand bien même ils auraient les compétences pour le faire.
Comme tout le monde n’a pas vocation à devenir informaticien développeur, il n’est pas nécessaire d’imposer à chacun de savoir coder.
Par contre, expliquer en classe comment fonctionne un ordinateur, ce qu’est un logiciel, comment il est conçu et réalisé, me parait être une très bonne chose, au même titre qu’expliquer le principe de fonctionnement d’une voiture hybride ou d’un congélateur. Nous vivons dans une société technologique dans laquelle avoir une culture scientifique et technique est un atout. Et puis l’école devrait être un lieu où chaque enfant progresse à son rythme, au mieux de ses possibilités, découvre et développe ses talents. Il me parait donc souhaitable que les enfants doués pour la conception technique, l’ingénierie, ou la programmation par exemple, puissent s’initier à ces domaines dans le cadre scolaire.